数学最显著的特点之一就是应用的极其广泛性。在我们日常生活的每一个角落里都可以找到数学的影子。在社会生活的各个领域里,都在运用着数学的概念,法则和结论。很多看似和数学无关的问题都可以运用数学工具加以解决。但在过去相当长的一段时间里,很多学生学习数学多年,并不知道数学有什么用途,他们认为数学是枯燥无味的,学习数学就是为了应付中考与高考。学生的想像力、创造力不仅得不到发挥。现在提倡素质教育,数学素养已成为公民文化素养的重要内容。素质教育在数学学科中的一个很突出的方面就是应用意识的培养。
数学模型是沟通实际问题与数学工具之间的桥梁。本文拟通过几个趣味数学应用的案例分析与数学建模,体现数学应用的广泛性,在一定程度上帮助数学爱好者看到数学生动、有趣、甚至于好玩的一面,以丰富数学学习的内容,提高中学生学习数学的积极性、主动性、探索性。
例1 证明任意的6个人中,必有3个人互相认识或者3个人互相不认识。
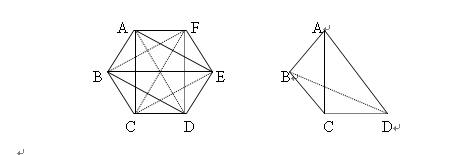
分析:用平面上的任意6个点(无三点共线)来代表6个人,两个人互相认识则在两点之间用实线连接,两个人互相不认识则在两点之间用虚线连接。则此看似和数学无关的问题相当于:平面上有6个点(无三点共线),任意两点之间用实线或虚线连接,求证连接后的图形中存在实线或虚线三角形(如下左图示)。
证明:考察线段AB、AC、AD、AE、AF,其中至少有三条或同为实线或同为虚线,不妨设线段AB、AC、AD为实线。考察△BCD,若△BCD为虚线三角形,则此问题即得证,若△BCD不是虚线三角形,不妨设线段BC为实线,则△ABC即为实线三角形,此问题也得证(如下右图)。
例2 7只茶杯,杯口朝上,将其中的4只翻转过来(杯口朝上的变为杯口朝下,杯口朝下的变为杯口朝上),称为一次“运动”。试问:是否能经过有限多次的运动,使得茶杯的杯口全部朝下?
分析:将7只茶杯用字母分别表示为A1、A2、A3、A4、A5、A6、A7 ,茶杯的杯口朝上记为Ai=+1,杯口朝下记为Ai=-1(i=1,2,3,4,5,6,7),每次翻转其中的4只杯子的杯口方向,相当于7个字母中的4个字母取值改变符号,即相当于将其中的4个字母各乘以-1。问题归结为:已知7个字母A1、A2、A3、A4、A5、A6、A7,在开始时全部取值为+1,每次改变其中4个字母的符号,能否经过有限次,将7个+1变为7个-1?
解:考察经过第i(i=0,1,2,…n)次翻转的7个字母的乘积
Mi =A1A2A3A4A5A6A7,
开始的时候相当于7个字母取值全为+1,它们的积
M0 =A1A2A3A4A5A6A7=(+1)7=+1;
经过一次翻转后,
M1 =A1A2A3A4A5A6A7=M0(+1)4=+1;
经过两次翻转后,
M2 =A1A2A3A4A5A6A7=M1(+1)4=+1;
……
所以不论经过多少次翻转,7个字母的乘积保持不变,仍为+1。
另一方面,杯口全部朝下,相当于7个字母的取值勤全为-1,它们的乘积是-1。这就表明,经过有限次的翻转,7个+1不会变为7个-1。
因此,经过有限次的翻转,不能使7只茶杯的杯口全部朝下。
例3 某人于上午8点由山下出发,下午15点抵达山顶,第二天上午8点由山顶出发按原路返回,并于下午15点回到山下原出发点,问在两天的路线中是否存在这样一个点,该人经过此点时,两天中的手表指向同一时刻?
分析:这个问题初看起来不容易得到答案,换一个角度思考:把该人在两天中做的事移到一天中来做,设想将这个人再克隆出一个人来,上午八点时,该人由山下出发,而克隆人同时由山上出发,由于走的是同一条路线,因此该人与其克隆人必定在中途相遇,在相遇点处,则手表指向同一时刻。下面用数学工具证明之。
该问题与路线的形状无关,不失一般性,不妨行走的路线为线段AB,行走的时间t为位置x的连续函数 第一天,A→B设t=f(x)(A≤x≤B),且f(A)=8,f(B)=15;第二天,B→A设t= g(x)(A≤x≤B),g(A)=15,g(B)=8;问题归结为,已知连续函数f(x)、g(x)(A≤x≤B),且f(A)=8,f(B)=15; g(A)=15,g(B)=8。求证:存在一点x 0(A≤x 0≤B),使得f(x 0)=g(x 0)。
证明:设h(x)=f(x )-g(x ) (A≤x≤B),则h(x)也是连续函数,且h(A)=f(A )-g(A )= 8-15=-7<0,h(B)=f(B )-g(B )= 15-8>0,因此在区间 [A,B] 内至少存在一点x 0,使得h(x 0)=f(x 0)-g(x 0)=0,即f(x 0)=g(x 0)。
例4 三名商人各带一个仆人乘船过河,一只小船只能容纳二人,由他们自己划行,仆人们事先秘密约定,在河的任一岸,一旦仆人的人数比商人多,就杀人越货。但是如何乘船渡河的大权掌握在商人们手中,商人们应该怎么设计安全过河的方案呢?
分析:用k(k=1,2,……,n)表示渡河的次数,记第k 次渡河前此岸的商人数为xk,仆人数为yk,(xk,yk)表示的是第k 次渡河前此岸的状态, ( xk,yk=0,1,2,3);开始渡河前的状态为(3,3),最终目标状态为(0,0)。
将(xk,yk)视为平面上的点的坐标,在xoy平面坐标系上画出下左图,(xk,yk)就是图中的方格线交叉点,共有16个点,其中某些点是安全状态,某些点不是安全状态,例如:(2,1)表示的是此岸上有2个商人、1个仆人,但对岸上则是1个商人、2个仆人,则点(2,1)不是安全状态。安全状态点共有10个(下左图中标出的黑点),为:
{(xk,yk)| (xk=0,yk=0,1,2,3;xk=3,yk=0,1,2,3;xk=yk=1或2;)
k为奇数时,船从此岸驶向彼岸,此岸人数减少,减少的人数为小船上运走的人数,由题设,小船每次最多装2个人,此时状态由(xk,yk)→(xk+1,yk+1), 这相当于将点(xk,yk)沿方格线向下或向左移动1~2格 ,移到(xk+1,yk+1)。
k为偶数时,船由彼岸驶回此岸,此岸人数增加,增加的人数为小船上运来的人数,此时状态由(xk,yk)→(xk+1,yk+1),这相当于将点(xk,yk)沿方格线向上或向右移动1~2格,移到(xk+1,yk+1)。
由上面的分析可知:制订安全渡河方案归结为如下的问题:将点(3,3)经过图中那些安全状态点进行有限次移动, 移动的次数k为奇数时,沿方格线向左或向下方移动1或2格;移动次数 k为偶数时,沿方格线向右或向上方移动1或2格。经过有限次移动,最终移至原点(0,0)。
编一段程序用计算机求解上述问题是可行的。不过对于商人和仆人人数不大的简单状况,用图解法解这个模型更为方便。
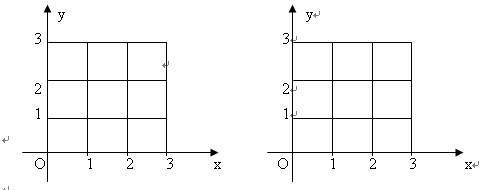
上图给出了一种移动方案,这个结果很容易翻译成渡河的方案:
(3,3)(2个仆人过河)→(3,1)(1个仆人返回)→(3,2)(2个仆人过河)→(3,0)(1个仆人返回)→(3,1)(2个商人过河)→(1,1)(1个商人1个仆人返回)→(2,2)(2个商人过河)→(0,2)(1个仆人返回)→(0,3)(2个仆人过河)→(0,1)(1个仆人返回)→(0,2)(2个仆人过河)→(0,0)。
大连教育学院 蒋永晶
